Power laws & the new science of complexity management
In an intricately networked world, the study of “nonequilibrium” systems is teaching companies how to overcome risk.
(originally published by Booz & Company)
 |
|
Illustration by Guy Billout |
Today, science is increasingly concerned with understanding not only how more is different, but how “more” becomes “different” — how thousands of genes and proteins interact to create the human organism, or how an ant colony organizes its members into an intelligent community. This research, broadly associated with the term complexity science, is gathering attention in the business world as well, as executives and scholars recognize that conventional theories of management, forged in the era of industrialization, vertically integrated companies, and relatively impermeable institutional borders, can no longer cope with the immensely complex organizations that have emerged during two decades of rising globalization and decentralization. With the global economy now far more integrated than it has ever been, chains of economic cause and effect reach across the world with disconcerting speed, exposing individuals, firms, and governments to a new kind of “interdependence risk” — to the possibility that events quite far away can undermine the activities on which their security and prosperity depend.
Does the specter of ever-increasing complexity mean senior executives must succumb to rising unpredictability, uncertainty, and loss of managerial control? Not necessarily. During the three decades of its development, complexity science has not only chronicled the phenomenon of interdependence: It has also opened paths to understanding and handling its challenges. Although complex systems are frequently unpredictable — inevitably so, in many instances — they also exhibit precise regularities. Relatively simple patterns, known as power laws and observed in disparate settings from astrophysics to evolutionary biology, as well as in human society, suggest strategies by which well-managed organizations can deal with uncertainty and navigate the discontinuities of contemporary business.
Modern science has moved well beyond a fixation on exact prediction and control; it has learned to accept unpredictability as an unavoidable and, at times, even beneficial aspect of the world, as a resource that can sometimes be harnessed. Businesses can also learn to adapt to complexity, in ways that can help them both reduce risk and expand opportunities.
The Simplicity Behind
From trees and coastlines to the rough surface of a broken brick, the natural world is at home with irregularity. Many natural structures violate the tidy principles of Euclidean geometry and appear to lack any identifiable order. However, as mathematician Benoit Mandelbrot pointed out decades ago, they do possess a kind of hidden organization. Small portions of a tree or a cloud or a brick’s fractured surface resemble larger parts, and these larger parts in turn resemble the whole. Irregular structures in nature are often “self-similar” in this way; they are what Mandelbrot called fractals.
Physicists have learned that hidden order of this sort comes with a very simple mathematical signature. A power law is a relationship in which one quantity A is proportional to another B taken to some power n; that is, A~Bn. Trees, clouds, and fractured surfaces all conform to power laws, as do river drainage basins, fluctuations in Internet traffic, the response of the immune system, and a vast range of other natural phenomena. Surprisingly, power laws also arise in the statistics of events that would seem to be utterly random, such as earthquakes and forest fires. For example, the number of earthquakes that release energy E — a measure of their strength — is simply proportional to 1/E2.
These findings reflect a simplicity that lurks behind complexity, and they hold fundamental importance for modern science. For a century or more, physics has focused principally on systems in “equilibrium”; indeed, virtually everything we know about the properties of ordinary substances, from metals to liquid crystals, from semiconductors to superfluids, rests on equilibrium theories. So do many of the more “exotic” applications of physics to such areas as quantum computation. In sharp contrast, power laws emerge naturally in systems that are decidedly not in equilibrium, such as the Earth’s crust or the Internet, which evolve perpetually and never settle into an unchanging state.
Complexity science has grown out of physicists’ attempts to build theories for this huge and largely unexplored area of “nonequilibrium” systems, with applications in physics, chemistry, and biology, but also in other settings, such as economics.
Firms, for example, also show power-law organization. In the United States, one might naturally assume that the diversity among more than 5 million commercial entities — publicly traded and privately held, as varied as oil companies, auto body shops, and dog-walking services — would make it nearly impossible to generalize about the scope of business. Yet sociologist Robert Axtell of the Brookings Institution, who has studied the empirical distribution of U.S. firms according to their total sales, has found a strikingly simple pattern: The number of firms having total sales S is proportional to 1/S2. In words, firms with sales of $1 million are four times as numerous as those with $2 million, which are four times as numerous as those with $4 million, and so on, right across the board for firms ranging from tiny news agents up to vast multinationals.
Distribution of wealth also conforms to a power law and proves empirically similar across many nations, despite different political orientations and economic foundations. The distribution of cities by population within any country also follows a power law, with the number of cities having N inhabitants being proportional to 1/N2. Or consider the financial markets. Exhaustive statistical studies have recently shown that the likelihood of a fractional change in price of amount f falls off as 1/f4, with this simple regularity holding for virtually all financial markets of all kinds and at all times. This means that for Microsoft, or General Electric, or any other stock, a 1 percent change (up or down) is precisely 16 times as likely as a 2 percent change, which itself is 16 times as likely as a 4 percent change, and so on, right across the board. Price changes may be largely random, yet they also reveal a surprising order.
What Is Normal?
Power laws reflect a pattern of organization and change that is typical for complex systems. Hence, familiarity with their properties offers some clues to the expected character of any complex system — including the modern business environment. Systems that follow power laws defy our intuitive expectations in surprising ways.
If you set 500 salespeople to work independently on the telephones, then, according to the “bell curve” of mathematics, their total weekly sales will almost always fall within a narrow range around some average; large deviations are exceedingly rare. The bell curve reflects a baseline theory for what happens when many independent events contribute to some outcome. It is what makes past averages of everything from corporate earnings to a baseball player’s batting percentage useful as guides to the future.
But the Achilles’ heel of the bell curve is the word independent. When one event influences another, we enter the world of interdependence, where the bell curve does not apply. Consider our salespeople again. In real companies, members of the sales force rarely act completely independently. They are likely to be members of a product group, or a regional body; they meet to agree on goals and compare tactics, and they compete for bonuses. In short, what one person does has the potential to influence the behavior of others, leading to collective swings in sales effectiveness.
When interdependence is important, the power-law pattern frequently takes the place of the bell curve. At first glance, this may not seem very important, as the two curves do not appear to be that different. But on closer scrutiny, there is actually an enormous difference. The “tails” of a power-law curve — the regions to either side that correspond to large fluctuations — fall off very slowly in comparison with those of the bell curve. (See Exhibit 1.) These so-called fat tails imply that large events take place far more often than one would expect on the basis of “normal” statistics. In the case of market fluctuations, for example, the bell curve predicts a one-day drop of 10 percent in the valuation of a stock just about once every 500 years. The empirical power law gives a very different and more reliable estimate: about once every five years.
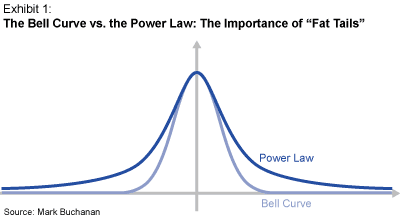
Large disruptive events are not only more frequent than intuition might dictate, they are also disproportionate in their effect. In any decade, a handful of the largest earthquakes do more property damage than the rest put together. Similarly, most of the total movement in any stock over a single year is often attributable to abrupt changes on a few select days. As a consequence, a plot of the typical rhythm for a power-law system shows a wild, fluctuating pattern, with a few huge peaks standing out against a background of relative quiet. In the context of evolutionary biology — where it is known that mass extinctions follow a power law, with many small events and a handful of massive cataclysms — this vision of what is normal has been referred to as “punctuated equilibrium.” Whatever the system, a power law points to a distinctive pattern of this sort, in which abrupt and violent transitions separate epochs of relative quiescence.
Power laws are normal for many complex systems. As a general rule, we should expect change to arrive not in the form of simple linear trends or dependable cycles, which naturally feed our craving for security, but in a far more erratic and unpredictable way. For a business, this perspective suggests that most of the risk it faces should be tied up with relatively infrequent and unpredictable events that alter its environment in a significant way. We might refer to this as “discontinuity” risk. Well-managed organizations are learning how to deal with it.
Reasoning with Extremes
The most famous financial mishap in recent history can be attributed to an inadequate appreciation for the consequences of power-law fluctuations. In 1994 and 1995, the hedge fund Long-Term Capital Management (LTCM) returned net profits of more than 40 percent, and by early 1998, it had increased its portfolio of assets to $1.3 billion. To many, it seemed as if LTCM, a company founded by former Salomon Brothers bond trader John Meriwether, with a board that included Nobel Prize–winning economists Myron Scholes and Robert Merton, had learned the secret for pumping money out of markets without risk.
Unfortunately for fund investors, LTCM’s assessment of the potential for overall losses was effectively built on the bell curve. A common technique in risk management is to estimate how much money the fund has a 1 percent (for example) chance of losing. This is known as the Value at Risk (VaR) and offers a rough measure of how much an investor might actually lose if things go badly.
Yet VaR estimates based on the bell curve can be wildly low. In fact, fund managers at LTCM were sophisticated enough to be aware that their bell curve estimates were probably low, yet they lacked methods for assessing the likelihood of more extreme risks. In September of 1998, “unexpected” volatility in the markets, set off by a default in Russia’s sovereign debt, led LTCM to lose more than 90 percent of its value. LTCM had borrowed more than $125 billion; the reverberations of its loss were felt across the global economy. To circumvent a more widespread collapse in the financial markets, the Federal Reserve Bank of New York organized a $3.6 billion bailout.
It is possible to deal with extreme financial risks in a more considered way. “LTCM’s risk management was appalling,” says statistical physicist Jean-Philippe Bouchaud, CEO of the Paris-based hedge fund Capital Fund Management (CFM). CFM relies on ideas from physics to take power-law fluctuations explicitly into account when building investment portfolios and when calculating VaR. Typically, the contract between a hedge fund manager and an investor states that the latter has a 1 percent chance of losing something like 10 percent of the total invested value. The manager has to make sure that this estimate of 10 percent is realistic. “The power law is much better than the bell curve at establishing this risk,” says Dr. Bouchaud. It is also better at helping hedge fund managers avoid the painful consequences of “unexpected” fluctuations.
Over the past decade, physicists have been instrumental in drawing attention to the power-law character of financial returns and its implications. “Physicists have taken the fat tails seriously,” says Doyne Farmer of the Santa Fe Institute, another pioneer in the study of complexity. Physicists have also explored power-law implications in other areas such as portfolio optimization and option pricing. But this “heads-up” approach to extreme fluctuations has yet to penetrate to the core of international finance. Partly in response to the LTCM debacle, the Basel II accord on international banking, currently under development, will require financial institutions to set aside larger capital reserves to protect against surprises.
Unfortunately, the analysis behind these guidelines remains firmly based on the bell curve. “They just add a large fudge factor at the end,” Dr. Bouchaud complains. It would be more appropriate, he suggests, for the empirical reality of market fluctuations — as captured by the power law for financial returns — to be incorporated in the analysis of banking risk from the outset.
The insurance industry is facing a similar challenge to reorient itself toward discontinuity risks. Chris Barton, a research geologist with the U.S. Geological Survey, has studied insurance losses due to extreme weather events. If these followed the bell curve, then insurance companies would legitimately be able to estimate future claims on the basis of an average over past claims. But the data for extreme weather events instead shows a power law — extreme losses are far more common than one might expect. In one such event, in August of 1992, Hurricane Andrew smashed through southern Florida and Louisiana, creating insured losses exceeding $16 billion and total losses of more than $30 billion, even though the worst part of the storm missed Miami. This one event bankrupted several insurance companies and significantly depleted the insurance capital available for natural catastrophes.
Several experts have concluded in a review of the situation that “the basic assumptions underpinning most of the insurance industry are violated by the laws of nature that apply to climate and tropical cyclones.” The bell curve does the job with automobile insurance and other risks that reflect independent events, but it fails miserably when assessing large catastrophic losses due to hurricanes and earthquakes. Like the financial industry, however, the insurance industry is learning to plan for dramatic discontinuities. New financial instruments such as catastrophe bonds now help to spread risk into the capital markets, where resources are adequate to cover the potentially massive losses — as high as $100 billion — associated with a hurricane hitting a major city in the U.S.
Dealing with Discontinuity
Even in situations where a power law is not clearly evident — as in most real-world business settings — one can expect abrupt discontinuities to define the rhythm of the unfolding future. Many executives recognize that the greatest risks they face are those associated with these singular events — with the sudden loss of a major earnings driver, market destabilization linked to new technology, or unexpected governmental regulation. Successful companies have learned how to manage and prepare for discontinuities and recognize that these events also offer opportunities, as their competitors may take a big hit.
For example, the consensus among scientific experts is that human actions have probably affected the world’s climate, and that the environmental and social consequences could be dramatic and costly. For business, and especially energy companies, the risk associated with global climate change is much more immediate. Even in the absence of marked environmental change, a sudden and dramatic change in public opinion alone could have immense repercussions. As Robert Lukefahr and Tim Donohue recently reported in strategy+business, even a 30 percent drop in oil demand “would make development of reserves outside the Middle East — that is, practically all the reserves held by public companies — uneconomical.” (See “Global Warming: Perception Is Reality,” Fourth Quarter 2002.)
Some companies, such as BP, have effectively planned to protect themselves against this extreme risk. BP has diversified its interests and is now the world’s largest manufacturer of solar-powered devices. Meanwhile, it has become heavily involved in natural gas, which produces a relatively light load of greenhouse gases in comparison with other fossil fuels. Many other energy companies have not adopted measures to improve their resilience, and appear to believe — or hope — that the future will unfold slowly enough to allow high-risk events to be dealt with as they happen.
Some firms have learned to capitalize more directly by harvesting the lucrative returns associated with some discontinuities. In many industries, a few products dominate all others in terms of their returns on research and development investment. Think films or books, toys or pharmaceuticals, where many products have extremely low sales, while a few blockbusters reap massive rewards. One strategy in such industries may be to produce a broad spectrum of quick-to-market experimental products, to discover and exploit opportunities presented by market discontinuities.
Capital One, for example, customizes its credit card products by carrying out “experiments” with many thousands of proposed new products each year. Each of these proposed products is “tested” with the help of customer information to rate its attractiveness and potential for producing profits. Most of these new products are outright failures and never get beyond the computer, yet a few succeed, and once in a while, the company achieves a great breakthrough that makes the entire process worthwhile. From 1992 to 1998, Capital One grew from 1.5 million to nearly 17 million cardholders, largely on the back of a single breakthrough innovation, the balance transfer offer, which it introduced in 1992.
This exploratory strategy is similar to that used by a population of bacteria upon entering a harsh environment. Under such conditions, the population will produce a large number of highly mutated offspring. Most will not be viable and, along with the original population, will perish quickly. But a few mutants may hit on characteristics that enable them to thrive in the new environment. Their success will guarantee the continued existence of the population, which has now adapted itself to the new conditions.
Learning to deal with discontinuity requires more than mere diversification or efficient exploration of possible products, of course. It often — if not always — means that individuals and organizations face the difficult task of thinking differently; of breaking habits and questioning long-standing conceptual and cultural commitments. David Snowden, director of IBM’s new Cynefin Centre for Organisational Complexity in Cardiff, Wales, points out that “the entrainment of thinking” is a common problem. Ideas and practices that have proven effective in the past become akin to accepted norms; they acquire inertia, and often for a very good reason. On-the-fly experimentation in the real world is a dangerous thing; hence, we naturally cling to ideas that have worked before. “We do this in order to survive,” says Mr. Snowden.
But this pattern of behavior also leads to serious maladaptation in times of rapid change and crisis; it is most dangerous precisely during those moments of discontinuity that define the critical episodes of change in most complex systems. Part of the aim of Mr. Snowden and his colleagues at Cynefin is to create organizational tools that can be used to train individuals and groups to be prepared for these discontinuities.
“We call it immunization,” says Mr. Snowden. “We need to dip people into chaos on a regular basis.” In his view, no individual or unit should work within the context of a fixed or narrowly defined task for more than 18 months before being tossed into a radically new task and environment. Such frequent disruption-by-design of behavioral patterns keeps individuals and organizations alert and responsive to a changing environment.
Interdependence Risk
The risk associated with business discontinuity has an added dimension in today’s increasingly networked world. The modern extended enterprise not only benefits from improved efficiency and flexibility, but also faces qualitatively new risks associated with dependence on distant suppliers, financial institutions, other governments, and additional uncontrollable elements outside itself. Interdependence carries its own kind of risk, as it can project the consequences of distant discontinuities into one’s own backyard.
In the spring of 2000, when a fire took a single semiconductor plant out of action in New Mexico, Telefon AB L.M. Ericsson of Sweden came up millions of chips short while trying to launch a new mobile-phone product, and was ultimately driven out of the handset market. In 2002, a labor slowdown at ports on the West Coast cost U.S. businesses up to $1 billion per day for several weeks, bringing into sharp relief their dependence on facilities they do not themselves control. As in the case of financial investments, or insurance, one way to deal with such risk is to identify weak spots and to protect them with old-fashioned hardening of facilities or by building in redundancy or diversification. Network theory, another area within complexity science that has made impressive progress in the past few years, can also help to identify key operational hubs or bridging links within a supply chain that need to be protected.
But it is important to recognize that troubles associated with interdependence can have extremely subtle causes, and in some cases cannot be traced to any one element in a system. To illustrate, consider the flow of traffic. On any highway, if the density of traffic is fairly low, traffic flows smoothly. As the density increases, however, trouble can set in. If one car touches its brakes — for whatever reason — a car directly behind may also slow down, possibly triggering a third to do the same and causing a local traffic jam. We’ve all experienced these “phantom” jams, which arise out of nowhere, and then dissolve just as mysteriously. They are not anyone’s fault, but reflect a fundamental coordination problem arising from the inability of drivers to respond instantaneously to changes in their environment.
In 1995, physicists Kai Nagel and Maya Paczuski, both then at Brookhaven National Laboratory in Brookhaven, N.Y., explored this phenomenon in a beautiful series of simulations. Using a computer to model a single lane of traffic, they found that as traffic density increases, the flow eventually reaches a critical point of extreme instability. At this point, traffic flow is highly erratic; the distribution of traffic jams over time follows a power law, with immense jams taking place far more frequently than the bell curve would predict. On the face of it, this would seem to be a bad situation. But it turns out that this highly irregular state is also the most efficient for getting cars down the highway in this relatively simple single-lane model. Paradoxically, decreasing the traffic density to achieve a more uniform flow also leads to a decrease in the overall traffic flow (the number of cars passing by per hour).
This example may be more than illustrative, for traffic flow is not too different from the flow of products and materials through extended supply chains. In fact, physicist Dirk Helbing of the Dresden University of Technology has recently developed equations to model the dynamics of supply chains and found them to be nearly identical to those used to model traffic. Intriguingly, computations based on these equations show that interdependence within supply chains can stir up natural disruptions much like traffic jams. In essence, small variations in demand at the end of a supply chain tend to travel back upstream, growing in severity as they do and leading to sizable disruptions.
“Stop-and-go traffic,” Dr. Helbing comments, “emerges as drivers react with a time delay to a changing traffic situation in front. The frequently observed instability of supply chains occurs for similar reasons.” This natural and “emergent” instability has the potential to disrupt even the most closely managed supply chains, despite all the advances of recent years in Web-based information transfer to improve coordination.
In recent years, consultants have noted a trend — that as organizations become more efficient, they also seem to become more susceptible to small variations. This observation fits in well with Dr. Helbing’s findings, as well as the earlier work of Dr. Nagel and Dr. Paczuski. Driving the flow to be more efficient necessarily implies a lower margin for error, which brings greater instability and fluctuation in its wake. To counter this trend, it is important to find factors that can be used to control the complex, emergent dynamics of supply networks. Complexity science is no panacea, but it does suggest a way of thinking that can lead to success.
In Dr. Helbing’s model, managerial control enters through what he calls a control function, which reflects the strategy that a production manager uses in trying to adapt to varying demands and supplies. This strategy may well include information collected from the entire supply network, not only in the vicinity of one manufacturer. In studying the consequences of changes in this control strategy, Dr. Helbing has not found any one recipe for success. But what is important, he points out, is the finding that “small changes in strategy may have tremendous effects.” A slight increase in the time required to adapt production rates to a changing demand, for example, may suffice to push the system past a “tipping point” where small fluctuations suddenly explode into larger and more costly disruptions.
Dr. Helbing suggests that “these oscillations can be mitigated or even suppressed” with suitable strategies. But crafting the right strategy in the context of any particular supply line will almost certainly require a detailed exploration of its dynamics, most likely based on computational simulations that make it possible to explore emergence in a systematic way.
Investing in such exploration can pay high dividends, as Infineon Technologies in Dresden found last year when it hired Dr. Helbing to explore disruptions due to scheduling conflicts in its complex manufacturing lines for semiconductor chips. In collaboration with his student Dominique Fasold, Dr. Helbing discovered a counterintuitive but highly successful scheduling strategy that increased chip throughput by 30 percent. To put the potential of this approach in perspective, Intel estimates that similar optimization of its supply lines could save the company several billion dollars each year.
Living with Complexity
The power laws of complexity science reveal that regularity and predictability are neither as regular nor as predictable as business leaders have come to believe. Power laws suggest that today’s organizations, in following modern science beyond a misplaced fixation on predictability, face three closely related tasks:
-
To follow the financial and insurance industries in taking the “fat tails” of power law systems seriously. Expect change to arrive not gradually, in a way that will allow the organization to adjust in real time, but in sudden discontinuities of great consequence that reshape the business environment, bringing both dangers and opportunities.
-
To recognize that globalization and decentralization bring risks as well as rewards, and that more is sometimes different — that increased interdependence can create the conditions for “emergent” threats that are traceable to no specific element within the system.
-
To take note of the human element in efforts to become adaptable, in part by organizing practices to decrease “entrainment of thinking.”
Management used to mean finding solutions. Using physics, engineers could solve equations and learn how to control processes in the manufacturing of materials, in chemical processing, or what have you. In operations research, managers adopted the same mind-set, aiming to find optimal solutions to scheduling problems or supply chain management. The recipe was simple, traditional, and straightforward: identify the problem, solve it, and then apply the solution.
Today, there are fewer certainties. Unfortunately, our habits of thought still make us look for linear trends and other simple patterns, and make us expect the future to be a recognizable version of the past. In many cases, we constrain our lives in an attempt to achieve such security, but in complex networks of competing businesses, in financial markets, in the world of emerging technology, and in politics, these expectations are out of place.
Organizations need to learn to distinguish between the kinds of problems that can be handled with traditional perspectives, where precise prediction and solution is possible, and the kinds of problems associated with unavoidable complexity. Entrainment of thinking is an ever-present danger. Early last century, Frederick Taylor applied Newtonian physics, the science of his day, to management. One hundred years later, as Mr. Snowden laments, “We haven’t yet grown out of this.” ![]()
Reprint No. 04107
Mark Buchanan (mark.buchanan@wanadoo.fr) is the author of Nexus: Small Worlds and the Groundbreaking Science of Networks (W.W. Norton, 2002) and Ubiquity: The Science of History, or Why the World Is Simpler Than We Think (Random House, 2001). Formerly an editor with Nature and New Scientist, he holds a Ph.D. in physics from the University of Virginia.


